Code Optimization | Code Optimization Techniques

Code Optimization-

Code Optimization is an approach to enhance the performance of the code.

The process of code optimization involves-

• Eliminating the unwanted code lines
• Rearranging the statements of the code

Advantages-

The optimized code has the following advantages-

• Optimized code has faster execution speed.
• Optimized code utilizes the memory efficiently.
• Optimized code gives better performance.

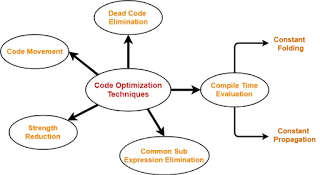
Code Optimization Techniques-

Important code optimization techniques are-

1. Compile Time Evaluation
2. Common sub-expression elimination
3. Dead Code Elimination
4. Code Movement
5. Strength Reduction

1. Compile Time Evaluation-

Two techniques that falls under compile time evaluation are-

A) Constant Folding-

In this technique,

• As the name suggests, it involves folding the constants.
• The expressions that contain the operands having constant values at compile time are evaluated.
• Those expressions are then replaced with their respective results.

Example-

Circumference of Circle  = (22/7) x Diameter

Here,

• This technique evaluates the expression 22/7 at compile time.
• The expression is then replaced with its result 3.14.
• This saves the time at run time.

B) Constant Propagation-

In this technique,

• If some variable has been assigned some constant value, then it replaces that variable with its constant value in the further program during compilation.
• The condition is that the value of variable must not get alter in between.

Example-

pi = 3.14

radius = 10

Area of circle = pi x radius x radius

Here,

• This technique substitutes the value of variables ‘pi’ and ‘radius’ at compile time.
• It then evaluates the expression 3.14 x 10 x 10.
• The expression is then replaced with its result 314.
• This saves the time at run time.

2. Common Sub-Expression Elimination-

The expression that has been already computed before and appears again in the code for computation

is called as Common Sub-Expression.

In this technique,

• As the name suggests, it involves eliminating the common sub expressions.
• The redundant expressions are eliminated to avoid their re-computation.
• The already computed result is used in the further program when required.

Example-

Code Before Optimization Code After Optimization

S1 = 4 x i S1 = 4 x i

S2 = a[S1] S2 = a[S1]

S3 = 4 x j S3 = 4 x j

S4 = 4 x i  // Redundant  Expression S5 = n

S5 = n

S6 = b[S4] + S5 S6 = b[S4] + S5

3. Code Movement-

In this technique,

• As the name suggests, it involves movement of the code.
• The code present inside the loop is moved out if it does not matter whether it is present inside or outside.
• Such a code unnecessarily gets execute again and again with each iteration of the loop.
• This leads to the wastage of time at run time.

Example-

Code Before Optimization Code After Optimization

for ( int j = 0 ; j < n ; j ++) x = y + z ;

{ for ( int j = 0 ; j < n ; j ++)

x = y + z ; {

a[j] = 6 x j; a[j] = 6 x j;

} }

4. Dead Code Elimination-

In this technique,

• As the name suggests, it involves eliminating the dead code.
• The statements of the code which either never executes or are unreachable or their output is never used are eliminated.

Example-

Code Before Optimization Code After Optimization

if (i == 1) i = 0

{

a = x + 5 ;

}

i = 0 ;

5. Strength Reduction-

In this technique,

• As the name suggests, it involves reducing the strength of expressions.
• This technique replaces the expensive and costly operators with the simple and cheaper ones.

Example-

Code Before Optimization Code After Optimization

B = A x 2 B = A + A

Here,

• The expression “A x 2” is replaced with the expression “A + A”.
• This is because the cost of multiplication operator is higher than that of addition operator.