Skip to main content

Ambiguous Grammar | Grammar in Automata

Before you go through this article, make sure that you have gone through the previous article onTypes of Grammarin Automata.

On the basis of number of derivation trees, grammars are classified as-



  1. Ambiguous Grammar
  2. Unambiguous Grammar

1. Ambiguous Grammar-

A grammar is said to ambiguous if for any string generated by it, it produces more than one-

  • Parse tree
  • Or derivation tree
  • Or syntax tree
  • Or leftmost derivation
  • Or rightmost derivation

Example-

Consider the following grammar-
E → E + E / E x E / id
Ambiguous Grammar
This grammar is an example of ambiguous grammar.
Any of the following reasons can be stated to prove the grammar ambiguous-

Reason-01:

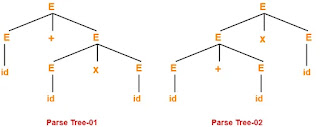
Let us consider a string w generated by the grammar-

w = id + id x id
Now, let us draw the parse trees for this string w.


Since two parse trees exist for string w, therefore the grammar is ambiguous.

Reason-02:

Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us draw the syntax trees for this string w.

Since two syntax trees exist for string w, therefore the grammar is ambiguous.

Reason-03:

Let us consider a string w generated by the grammar-
w = id + id x id
Now, let us write the leftmost derivations for this string w.


Since two rightmost derivations exist for string w, therefore the grammar is ambiguous.


2. Unambiguous Grammar-

A grammar is said to unambiguous if for every string generated by it, it produces exactly one-
  • Parse tree
  • Or derivation tree
  • Or syntax tree
  • Or leftmost derivation
  • Or rightmost derivation

Example-

Consider the following grammar-
E → E + T / T
T → T x F / F
F → id
Unambiguous Grammar
This grammar is an example of unambiguous grammar.

Comments

Post a Comment

Popular posts from this blog

Code Optimization | Code Optimization Techniques

Code Optimization- Code Optimization is an approach to enhance the performance of the code. The process of code optimization involves- Eliminating the unwanted code lines Rearranging the statements of the code Advantages- The optimized code has the following advantages- Optimized code has faster execution speed. Optimized code utilizes the memory efficiently. Optimized code gives better performance. Code Optimization Techniques- Important code optimization techniques are- Compile Time Evaluation Common sub-expression elimination Dead Code Elimination Code Movement Strength Reduction 1. Compile Time Evaluation- Two techniques that falls under compile time evaluation are- A) Constant Folding- In this technique, As the name suggests, it involves folding the constants. The expressions that contain the operands having constant values at compile time are evaluated. Those express...
Post a Comment
Read more

Elimination of Left Factoring

In left factoring, We make one production for each common prefixes. The common prefix may be a terminal or a non-terminal or a combination of both. Rest of the derivation is added by new productions. The grammar obtained after the process of left factoring is called as Left Factored Grammar . Example-   PRACTICE PROBLEMS BASED ON LEFT FACTORING- Problem-01: Do left factoring in the following grammar- S → iEtS / iEtSeS / a E → b Solution- The left factored grammar is- S → iEtSS’ / a S’ → eS / ∈ E → b Problem-02: Do left factoring in the following grammar- A → aAB / aBc / aAc Solution- Step-01: A → aA’ A’ → AB / Bc / Ac Again, this is a grammar with common prefixes. Step-02: A → aA’ A’ → AD / Bc D → B / c This is a left factored grammar. Problem-03: Do left factoring in the following grammar- S → bSSaaS / bSSaSb / bSb / a Solution- ...
Post a Comment
Read more

Testing a Program – An Example

Question: Write a set of test cases – specific set of data – to properly test a relatively Simple program. Create a set of test data for the program - data the program must handle correctly to be considered a successful program. Here’s a description of the program: “The program reads three integer values from an input dialog. The three values represent the lengths of the sides of a triangle. The program displays a message that states whether the triangle is scalene, isosceles, or equilateral”. Code: The function triangle takes three integer parameters that are interpreted as the lengths of the sides of a triangle. It returns whether the triangle is equilateral (three lengths equal), isosceles (two lengths equal), scalene (no lengths equal), or invalid (impossible lengths). Evaluate your test cases: Evaluate your set of test cases by using it to answer the following questions. Give yourself one point for each “YES” answer. Do you have a test case that represents a ...
Post a Comment
Read more